Correlatie gebruiken we om te onderzoeken of verband is tussen twee numerieke variabelen. Met correlatie toon je een statisch verband aan. De sterkte van deze samenhang wordt uitgedrukt in een correlatiecoëfficiënt.
Dit wil alleen niet zeggen dat er ook een causale relatie is. Een aangetoond statische verband zegt niet of er daadwerkelijk een oorzaak-gevolg relatie is tussen de variabelen.
Spurious correlations
Een aangetoond statische verband zegt dus niet of er daadwerkelijk een oorzaak-gevolg relatie is tussen de variabelen. Een leuk voorbeeld zie je hieronder:
Correlatie volgens Pearson
In dit artikel gaan we uit van de berekening volgens Pearson: het uitdrukken van een lineaire samenhang. De correlatie kan variëren tussen -1 en +1. Nul betekent geen samenhang, +1 betekent een 100% positieve samenhang en -1 een 100% negatieve samenhang. De afstand tot nul geeft de sterkte van de correlatie aan.
We gebruiken correlatie om te onderzoeken of twee variabelen met elkaar samenhangen.
Multicollineariteit
We spreken van multicollineariteit wanneer meerdere onafhankelijke variabelen onderling sterk gecorreleerd zijn. Onafhankelijke variabelen zijn de verklarende variabelen in een regressie model. Het maakt het inschatten van de relatie tussen elke variabele en de afhankelijke variabele (wat we willen voorspellen) moeilijker omdat de variabelen elkaar onderling beïnvloeden.
Een sterke multicollineariteit zorgt voor een toename in de variantie van de uitkomsten en maakt de uitkomsten gevoelig voor kleine wijzigingen in het model. De statische gevolgtrekking uit de data wordt minder betrouwbaar en uitkomsten van machine learning modellen minder stabiel.
Ben je een Python gebruiker?
Natuurlijk kan je dit artikel over R verder lezen en inspiratie op doen. Inmiddels heb ik ook een artikel geschreven over berekenen correlatie in Python: een verkennende data analyse naar correlatie tussen bijstand en werkloosheidscijfers.
Eenvoudig correlatie berekenen in R
De correlatie tussen twee variabelen kunnen we in R eenvoudig berekenen.
# Pearson is standaard. Gebruik ?cor voor meer opties
cor(huisprijzen.df$BedroomAbvGr,huisprijzen.df$SalePrice)
Voor de samenhang tussen meerdere variabelen gebruiken we een correlatiematrix.
# Alleen zinvol voor numerieke variabelen
variabelenNumeriek <- names(sapply(huisprijzen.df,is.numeric))
# De correlatie matrix:
corMatrix <- round(cor(huisprijzen.df %>% select(variabelenNumeriek)),2)
print(corMatrix)
In je RStudio console wordt daarna de correlatiematrix getoond:
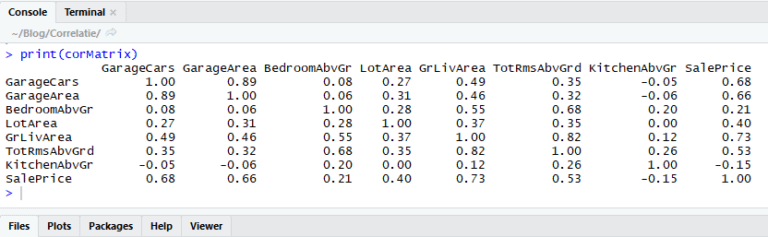
De samenhang die een variabele heeft met zichzelf is natuurlijk 1.00
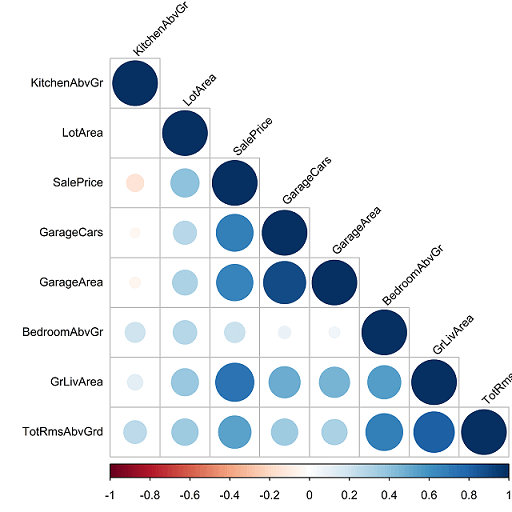
Plot je correlatiematrix met ‘corrplot’
Door de matrix te visualiseren zijn sterke verbanden beter te herkennen. We doen dit met package ‘corrplot’.
# package laden
require(corrplot)
# plot je plot met corrplot
corrplot(corMatrix,
title = "",
type = "lower",
order = "hclust",
hclust.method = "centroid",
tl.cex = 0.8,
tl.col = "black",
tl.srt = 45)
Hieronder wordt een voorbeeld weergegeven van een correlatiematrix gemaakt met ‘corrplot’. We kunnen eenvoudig zien dat er een sterk onderling verband is. Namelijk tussen de oppervlakte van garages en het aantal auto’s dat in een garage past. De leefoppervlakte heeft de sterkste samenhang met de verkoopprijs.
Wat zie jij nog meer?