Binnenkort gaan we in een project werken in een virtuele analyse omgeving voor exploratieve data analyse. En de standaard voor data analyse? Ja, Python. Tijd dus om beschrijvende statistiek en toetsen in Python uit te proberen.
Wist je dat de R datasets ook beschikbaar zijn in Python? In de lijst staat een dataset met lichaamstemperatuurmetingen van een bever. Waarbij wordt aangegeven of de bever in haar burcht was of daarbuiten.
Bevers behoren tot mijn favoriete dieren, de keuze was snel gemaakt. In dit artikel gaan we data visualiseren met Seaborn. Combineert uitstekend met bevers. Voor de statistische toetsen gebruiken we SciPy en statsmodels.
Python packages in dit artikel
from statsmodels import datasets # R datasets
import pandas as pd # data wrangling
import seaborn as sns # datavisualisatie
import matplotlib.pyplot as plt # datavisualisatie
import scipy.stats as stats # statistishe toetsen
from statsmodels.stats import diagnostic # statistishe toetsen
sns.set(rc={'axes.titlesize':16,'axes.labelsize':16}) # Template aanpassingen via rcParams
R datasets, ook in Python
Onze bever hebben we gevonden in R package ‘boot’. Met de get_rdataset() functie uit statsmodels laad je de dataset in Python. Er is ook documentatie beschikbaar waarin de dataset wordt beschreven. Handig! Nu weten we dat een ‘1’ in de kolom ‘activ’ inhoud dat onze bever buiten haar burcht is en dus waarschijnlijk activiteiten onderneemt met hoge intensiviteit. Bomen kappen en zo. In de burcht komen ze tot rust.
dataset_beaver = datasets.get_rdataset(
dataname='beaver', # Dataset naam
package='boot', # R package, herkomst dataset
cache=False
)
beaver = dataset_beaver.data # Datafram met de data
print(dataset_beaver.__doc__) # Documentatie tonen

Klein beetje data wrangling
beaver['activ'] = beaver.activ.map({1: 'Buiten', 0: 'Binnen'})
beaver = beaver.astype({'activ': 'category'})
beaver['time_bin'] = pd.qcut(beaver.time, q=6, precision=0) # wordt automatisch Dtype category
beaver.sample(2)
Pandas .describe(), handig maar mist iets
Snel een aantal beschrijvende statistieken over een dataset (DataFrame) tonen? Gebruik dan de Pandas functie describe(). De count toont het aantal rijen met een waarde. Zo heb je direct zicht op de lege waarden in jouw dataset. Standaard toont Pandas een statistische samenvatting van de numerieke en integer kolommen.
beaver.describe()
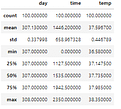
Categoriale data of datum kolommen
Er is ook een samenvatting beschikbaar voor categoriale data (nominaal of ordinaal) of datum. Je kan hiervoor een argument meegeven. De descibe() functie toont dan het aantal unieke waarden, de meest voorkomende waarde (top) en het aantal maal dat de modus voorkomt (freq).
beaver.describe(include=['category','object',
'string','datetime'])
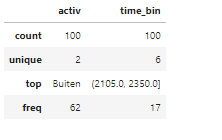
Beschrijvende statistiek met Pandas
Met de Pandas describe() functie krijg je eenvoudig een eerste indruk van de data. Deze statistische samenvatting kan je niet aanpassen. In deze paragraaf toon ik enkele voorbeelden over hoe je zelf beschrijvende statistieken kan berekenen door gebruik te maken van de beschrijvende statistieken, die standaard al in Pandas zitten. Mijn favorieten zijn:
- Gemiddelde (mean), mediaan (median) en standaard deviatie (std);
- Kwartielafstanden (quantile) en variatie (var);
- Minimum (min), maximum (max)en totaal (sum);
- Aantal gevulde waarden (count), meest voorkomende waarde (mode);
- Scheefheid (skew).
Hieronder als voorbeeld het berekenen van kwartielen en de interkwartielafstand (IQR):
kwartielen =beaver.temp.quantile([0.25,0.5,0.75])
IQR = beaver.temp.quantile(0.75) - beaver.temp.quantile(0.25)
print(kwartielen)
print(IQR)
Je eigen beschrijvende samenvatting samenstellen
Met Pandas agg() kan je een eigen beschrijvende samenvatting samenstellen, waarin je meerdere functies combineert:
beaver.agg({'temp': ['median', 'var',
'skew','kurt'],
'activ': ['mode']})

Met Pandas .groupby() kan je berekeningen maken per groep. Bijvoorbeeld de scheefheid (skewness) waarmee wordt aangegeven of een verdeling links of rechts scheef is ten opzichte van een normaalverdeling.
Is de uitkomst tussen de -0.5 en 0.5? Dan is de data waarschijnlijk normaal verdeeld. Kleiner dan -1 of hoger dan 1 wijst op een niet normale verdeling.
beaver.groupby('activ').temp.agg(['skew'])

Wil je een eigen berekening opnemen in een functie? Of een functie uitvoeren uit een ander Python package, bijvoorbeeld stats uit statsmodels? Gebruik dan niet de enkelvoudige quotes rond de functie namen. Het werkt als volgt:
# Populatie standaarddeviatie,
# Pandas geeft default de std van
# een steekproef
def populatie_std(x):
return x.std(ddof=0)
beaver.groupby('activ').temp.agg(['std',
populatie_std,
stats.iqr])

Kruistabel toont samenhang tussen tijd en activiteit
Onze bever heeft haar burcht gebouwd in noord-centraal Wisconsin. In de herfst gaat het al vroeg in de middag schemeren. Dat is het moment waarop bevers actief worden. Zien we deze samenhang terug in onderstaande kruistabel?
pd.crosstab(beaver.time_bin,
beaver.activ,
margins=True,
margins_name='Totaal')

Aanname van normaliteit, datavisualisaties met seaborn
Okay. We weten nu hoe we onze dataset kunnen beschrijven met relatief eenvoudige beschrijvende statistieken. Maar hoe zat het ook al weer met de aanname van normaliteit? Voorbeelden van geparametriseerde toetsen, die berusten op deze aanname zijn de t-toets en ANOVA. Na het lezen van ‘Assumption of Normality / Normality Test’ op statisticshowto.com, besluit ik om de lichaamstemperatuur eerst te visualiseren met een boxplot en een histogram. Daarna kunnen we de aanname van normaliteit bevestigen of verwerpen door een aantal toetsen uit te voeren.
fig, axs = plt.subplots(nrows=1, ncols=3,
figsize=(20,5),
constrained_layout=True)
sns.boxplot(y='temp', data=beaver, ax=axs[0])
sns.distplot(beaver.temp, hist=True, rug=True, ax=axs[1])
sns.boxplot(x='activ', y='temp', data=beaver, ax=axs[2])
axs[0].set_title('univariate boxplot')
axs[1].set_title('histogram')
axs[2].set_title('multivariate boxplot')
fig.suptitle('Spreiding en verdeling', fontsize=24)
plt.show()

g = sns.FacetGrid(beaver, col='activ',
margin_titles=True, height=5, aspect=2)
g.map(sns.distplot, 'temp', hist=True, rug=True)
g.fig.suptitle('Lichaamstemperatuur naar activiteit', fontsize=24)
plt.tight_layout()# constrained_layoute werkt niet voor FacetGrid
plt.subplots_adjust(top=0.8)
plt.show()

Als je kijkt naar de visualisaties valt het volgende op:
- De mediaan is in de boxplot links niet gelijk aan het midden. De mediaan lijn ligt niet in het midden van de box. Dit spreekt de aanname tegen.
- De boxplot links toont geen uitschieters (outliers).
- De histogram in het midden toont geen overduidelijke scheefheid, maar wel twee duidelijke pieken. Ik besluit om een extra boxplot (rechts) toe te voegen.
- De boxplot rechts toont dat er een duidelijk verschil is tussen de lichaamstemperatuur binnen en buiten. De histogrammen onderaan, tonen dat de lichaamstemperatuur buiten lijkt te voldoen aan een normaalverdeling.
Q-Q plot vergelijkt met normaalverdeling
Een Q-Q plot vergelijkt de kwartielafstanden van een normaalverdeling met de daadwerkelijke data. Bij een normaalverdeling zal de data de diagonale lijn volgen.
De lichaamstemperatuur buiten de burcht (plot rechts) komt het dichtste bij een normaal verdeling. Hoe interpreteer jij de Q-Q plot van de lichaamstemperatuur (plot links)?
buiten_temp = beaver.query("activ=='Buiten'").temp
binnen_temp = beaver.query("activ=='Binnen'").temp
fig, axs = plt.subplots(nrows=1, ncols=3,
figsize=(20,5),
constrained_layout=True)
stats.probplot(beaver.temp, dist="norm" , plot=axs[0])
stats.probplot(binnen_temp, dist="norm" , plot=axs[1])
stats.probplot(buiten_temp, dist="norm" , plot=axs[2])
axs[0].set_title('Lichaamstemperatuur')
axs[1].set_title('Lichaamstemperatuur binnen')
axs[2].set_title('Lichaamstemperatuur Buiten')
fig.suptitle('Q-Q plot lichaamstemperatuur', fontsize=24)
plt.show()

Toetsen in Python met SciPy of statmodels
We zijn nu een aantal paragrafen verder en waarschijnlijk komt nu de vraag op waar dit artikel naar toe gaat. In de praktijk willen we vaak weten of bepaalde groepen significant van elkaar afwijken. Bijvoorbeeld om onze dienstverlening beter af te stemmen op klantbehoeften of bepaald gedrag.
De lichaamstemperatuur van bevers zal hier waarschijnlijk niet aan bijdragen. Wel wordt oefenen een stuk leuker als de data je aanspreekt. We gaan nu verder met een T-test, waaruit zal blijken of de gemiddelde lichaamstemperatuur binnen versus buiten statistisch significant afwijkt.
T-toets, is het verschil in gemiddelde lichaamstemperatuur statistisch significant?
Independent T-test
Het vrouwtje in deze dataset is alleen. De historie van metingen is één dag. De onafhankelijke steekproeven zijn dus achter mijn netwerkpoortje blijven hangen. Ook zijn de metingen niet echt ‘paarsgewijs’. Stiekem, gaan we verder.
Gelukkig doet de ‘independent-samples t-test’, nog drie aannames over de data waar we wel wat mee kunnen. Het doel van dit artikel is niet purisme, maar de toepasbaarheid van Python voor statistische methodes.
Aanname 1: Geen significante uitschieters
In de boxplot over de lichaamstemperatuur binnen kan je zien dat er enkele uitschieters (outliers) zijn. Het verwijderen van deze datapunten is eenvoudig, soms te pragmatisch, maar voor nu afdoende. De code hieronder toont de uitschieters om deze vervolgens te verwijderen.
# Boxplot min en max
IQR = binnen_temp.quantile(0.75) - binnen_temp.quantile(0.25)
BoxplotMax = binnen_temp.quantile(0.75) + IQR * 1.5
BoxplotMin = binnen_temp.quantile(0.25) - IQR * 1.5
print(BoxplotMax)
print(BoxplotMin)
# Tonen van de outliers
mask = ((beaver.activ=='Binnen') & (beaver.temp > BoxplotMax)) | ((beaver.activ=='Binnen') & (beaver.temp < BoxplotMin))
beaver[mask]
# Outliers verwijderen
beaver.drop(beaver[mask].index, inplace=True)
Aanname 2: Ongeveer normaal verdeeld
In Scipy en statmodels zijn meerdere toetsen beschikbaar om data te toetsen op de aanname van een normaalverdeling. Gangbaar is om 0,05 als grens te nemen voor statistische significantie (p-waarde). De kans op toeval is dan kleiner dan 5%, en dus significant.
De scheefheid (skewness) van de lichaamstemperatuur doet vermoeden dat de data ongeveer normaal is verdeeld. Maar door de Q-Q van de lichaamstemperatuur ‘binnen’ ben ik gaan twijfelen. Daarom gaan we twee toetsen uitproberen om te testen of de data een normale verdeling volgt: de nul hypothese.
# Functie om gevonden p-waarde te vergelijken met
# threshold waarde: alpha.
def check_p_value(p_value, alpha=0.05):
if p_value <= alpha:
print("Nul hypothese verworpen." +
"\n"+ "(p-waarde = " + str(p_value) + ").")
else:
print("Nul hypothese geaccepteerd." +
"\n" + " (p-waarde = " + str(p_value) + ").")
Als de p-waarde kleiner is dan een vooraf gekozen waarde, een alpha tussen de 0.01 tot 0.1, dan verwerpen we de nul hypothese dat de data een normaal verdeling volgt.
P-waarde interpreteren
Lilliefors test uit Statmodels
# Binnen
p = diagnostic.lilliefors(binnen_temp,
dist='norm',
pvalmethod='table')[1]
check_p_value(p)
# Buiten
p = diagnostic.lilliefors(buiten_temp,
dist='norm',
pvalmethod='table')[1]
check_p_value(p)

Shapiro-Wilk test uit SciPy
# Binnen
p = stats.shapiro(binnen_temp)[1]
check_p_value(p)
# Buiten
p = stats.shapiro(buiten_temp)[1]
check_p_value(p)

Aanname 3: Homogeniteit van variantie
De Levene test wordt gebruikt om na te gaan of er sprake is van gelijkmatige variantie over verschillende groepen of steekproeven.
p = stats.levene(binnen_temp, buiten_temp, center='median')[1]
check_p_value(p)

Het duurde even, nu de Independent T-test zelf
Nu we de aannames hebben gecontroleerd, kunnen we de test zelf uitvoeren. Deze test vergelijkt de gemiddelden van twee groepen. Zoals eerder aangegeven kunnen we niet aannemen dat de groepen (binnen versus buiten) niet gerelateerd zijn. We hebben de hulp van één bever over een beperkte tijdspanne en als je warmer naar binnen gaat, dan is je lichaamstemperatuur binnen ook relatief hoger. Gelukkig is dit een vinger oefening en zijn de overige aannames t.o.v. de data dik in orde.
p = stats.ttest_ind(binnen_temp, buiten_temp, equal_var=True)[1] #
check_p_value(p)

De T-test toont dat de gemiddelden statistisch significant verschillen. De p-waarde is lager dan de gekozen alpha, dus verwerpen we de nul hypothese dat de gemiddelden binnen versus buiten gelijksoortig zijn. Deze uitslag verteld ons dat het verschil daadwerkelijk bestaat en niet op toeval berust. Een volgende stap kan zijn het onderzoeken van de effectgrootte.
Conclusie
Met beschrijvende statistiek in Python hebben we statistische significant onderbouwt wat we al wisten: als je bomen omhakt en dammen bouwt, dan heb je waarschijnlijk een andere gemiddelde lichaamstemperatuur dan thuis in je hol. Dat geldt dus ook voor bevers. Kunnen bevers ons helpen met statistiek? Zeer waarschijnlijk hebben ze geen interesse.
De dataset was een ludieke manier om kennis te maken met Python’s statistische packages: SciPy en Statmodels. In Python kan je bijna alle statistieken toepassen. Statistische data visualisatie is met Seaborn relatief eenvoudig.
Google ook eens op ‘Pingouin’. Dit nieuwe package maakt een aantal statistische bewerkingen een stuk eenvoudiger. Een mooie nieuwkomer!